2. Graphs

The problem needs to be modelled in such a way that a computer program can be applied to solve it. This modelling is done by the use of a graph structure. We have a section on graphs here. This is a typical graph

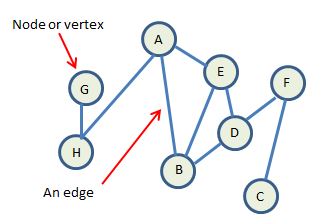
The graph represents an abstraction of the problem.

Each circle in the graph is called a vertex or node and they are labelled in some way to represent the data being modelled.

Each connection is called an edge.

In order to apply the graph to a path-finding algorithm, each edge needs to have some measure associated with it. This measure is called the cost.

For example a graph can be used to model a road network. Each vertex is a waypoint or location and each edge is a road. In this case the cost could be distance or it could be travel time. For example:

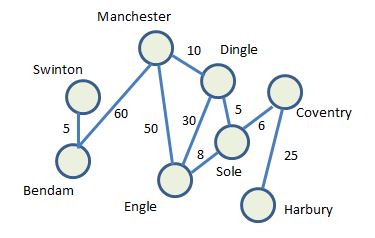
Having a value associated with each edge means that a least-cost path can be worked out. The nodes themselves could also have a cost associated with it. This kind of arrangement is called a weighted graph.

Furthermore, edge direction could be shown as arrows rather than lines, in which case it is a directed weighted graph.

The graph above is showing a single edge between nodes. With a directed graph, there could be two arrows indicating that cost may depend on direction. For example, below, if A,B is modelling a one-way street, going from A to B costs 5 but the other way is much more, indicating it is not a feasible path. You could even eliminate the backwards path to indicate it is not a legitimate path.

Graphs are very versatile in modelling search and optimisation problems and are widely used in fields such as artifcial intelligence.